Breadth First Search: Shortest Reach HackerRank Solution

Breadth First Search: Shortest Reach HackerRank Solution
Source : https://www.hackerrank.com/challenges/bfsshortreach

Consider an undirected graph where each edge is the same weight. Each of the nodes is labeled consecutively.

You will be given a number of queries. For each query, you will be given a list of edges describing an undirected graph. After you create a representation of the graph, you must determine and report the shortest distance to each of the other nodes from a given starting position using the breadth-first search algorithm (BFS). Distances are to be reported in node number order, ascending. If a node is unreachable, print for that node. Each of the edges weighs 6 units of distance.

For example, given a graph with nodes and edges, , a visual representation is:

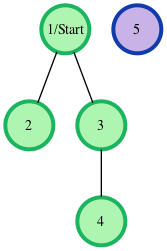
The start node for the example is node . Outputs are calculated for distances to nodes through : . Each edge is units, and the unreachable node has the required return distance of .

Function Description

Complete the bfs function in the editor below. It must return an array of integers representing distances from the start node to each other node in node ascending order. If a node is unreachable, its distance is .

bfs has the following parameter(s):

• n: the integer number of nodes
• m: the integer number of edges
• edges: a 2D array of start and end nodes for edges
• s: the node to start traversals from

Input Format

The first line contains an integer , the number of queries. Each of the following sets of lines has the following format:

• The first line contains two space-separated integers and , the number of nodes and edges in the graph.
• Each line of the subsequent lines contains two space-separated integers, and , describing an edge connecting node to node .
• The last line contains a single integer, , denoting the index of the starting node.

Constraints

Output Format

For each of the queries, print a single line of space-separated integers denoting the shortest distances to each of the other nodes from starting position . These distances should be listed sequentially by node number (i.e., ), but should not include node . If some node is unreachable from , print as the distance to that node.

Sample Input

2
4 2
1 2
1 3
1
3 1
2 3
2

Sample Output

6 6 -1-1 6

Explanation

We perform the following two queries:

1. The given graph can be represented as:
   
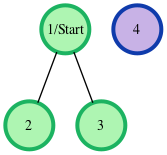
   where our start node, , is node . The shortest distances from to the other nodes are one edge to node , one edge to node , and an infinite distance to node (which it's not connected to). We then print node 's distance to nodes , , and (respectively) as a single line of space-separated integers: 6, 6, -1.

2. The given graph can be represented as:
   
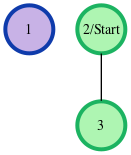
   where our start node, , is node . There is only one edge here, so node is unreachable from node and node has one edge connecting it to node . We then print node 's distance to nodes and (respectively) as a single line of space-separated integers: -1 6.

Note: Recall that the actual length of each edge is , and we print as the distance to any node that's unreachable from .

Source : https://www.hackerrank.com/challenges/bfsshortreach

Solution

	// Karthikalapati.blogspot.com
	import java.util.Scanner;
	import java.util.HashSet;
	import java.util.ArrayDeque;
	public class Solution {
	private static final int EDGE_WEIGHT = 6;
	public static void main(String[] args) {
	Scanner scan = new Scanner(System.in);
	int numQueries = scan.nextInt();
	for (int q = 0; q < numQueries; q++) {
	int numNodes = scan.nextInt();
	int numEdges = scan.nextInt();
	/* Create Nodes */
	Node [] node = new Node[numNodes + 1]; // node "i" will be at index "i"
	node[0] = null;
	for (int i = 1; i <= numNodes; i++) {
	node[i] = new Node(i);
	}
	/* Connect Nodes */
	for (int i = 0; i < numEdges; i++) {
	int n1 = scan.nextInt();
	int n2 = scan.nextInt();
	node[n1].addNeighbor(node[n2]);
	}
	/* Create MST */
	int start = scan.nextInt();
	findDistances(node[start]);
	/* Print results */
	for (int i = 1; i <= numNodes; i++) {
	if (i != start) {
	System.out.print(node[i].distance + " ");
	}
	}
	System.out.println();
	}
	scan.close();
	}
	/* Uses BFS to find minimum distance of each Node from "start".
	Can use BFS instead of Dijkstra's Algorithm since edges are equally weighted. */
	private static void findDistances(Node start) {
	if (start == null) {
	return;
	}
	ArrayDeque<Node> deque = new ArrayDeque(); // use deque as a queue
	start.distance = 0;
	deque.add(start);
	while (!deque.isEmpty()) {
	Node curr = deque.remove();
	for (Node neighbor : curr.neighbors) {
	if (neighbor.distance == -1) { // meaning it's unvisited
	neighbor.distance = curr.distance + EDGE_WEIGHT;
	deque.add(neighbor);
	}
	}
	}
	}
	/* Implementation of an UNDIRECTED graph */
	public static class Node {
	public final int id; // each Node will have a unique ID
	public int distance; // Also tells us if Node has been visited (-1 means unvisited)
	public HashSet<Node> neighbors;
	public Node (int id) {
	this.id = id;
	distance = -1;
	neighbors = new HashSet();
	}
	public void addNeighbor(Node neighbor) {
	neighbors.add(neighbor);
	neighbor.neighbors.add(this);
	}
	@Override
	public boolean equals(Object other) {
	if (other == this) {
	return true;
	} else if (other == null || !(other instanceof Node)) {
	return false;
	}
	Node otherNode = (Node) other;
	return this.id == otherNode.id;
	}
	@Override
	public int hashCode() {
	return id; // simple and effective
	}
	}
	}